Algorithm
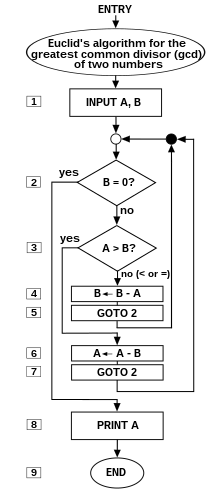
Flow chart of an algorithm (Euclid's algorithm) for calculating the greatest common divisor (g.c.d.) of two numbers a and b in locations named A and B. The algorithm proceeds by successive subtractions in two loops: IF the test B ≥ A yields "yes" (or true) (more accurately the number b in location B is greater than or equal to the number a in location A) THEN, the algorithm specifies B ← B − A (meaning the number b − a replaces the old b). Similarly, IF A > B, THEN A ← A − B. The process terminates when (the contents of) B is 0, yielding the g.c.d. in A. (Algorithm derived from Scott 2009:13; symbols and drawing style from Tausworthe 1977).
In mathematics and computer science, analgorithm (/ˈælɡərɪðəm/ ( listen) AL-gə-ridh-əm) is an unambiguous specification of how to solve a class of problems. Algorithms can perform calculation, data processing andautomated reasoning tasks.
listen) AL-gə-ridh-əm) is an unambiguous specification of how to solve a class of problems. Algorithms can perform calculation, data processing andautomated reasoning tasks.
An algorithm is an effective method that can be expressed within a finite amount of space and time[1] and in a well-defined formal language[2] for calculating a function.[3]Starting from an initial state and initial input (perhaps empty),[4] the instructions describe acomputation that, when executed, proceeds through a finite[5] number of well-defined successive states, eventually producing "output"[6] and terminating at a final ending state. The transition from one state to the next is not necessarily deterministic; some algorithms, known as randomized algorithms, incorporate random input.[7]
The concept of algorithm has existed for centuries and the use of the concept can be ascribed to Greek mathematicians;[8] the termalgorithm itself derives from the 9th Century mathematician Muḥammad ibn Mūsā al'Khwārizmī, latinized 'Algoritmi'. A partial formalization of what would become the modern notion of algorithm began with attempts to solve the Entscheidungsproblem(the "decision problem") posed by David Hilbert in 1928. Subsequent formalizations were framed as attempts to define "effective calculability"[9] or "effective method";[10] those formalizations included theGödel–Herbrand–Kleene recursive functionsof 1930, 1934 and 1935, Alonzo Church'slambda calculus of 1936, Emil Post's "Formulation 1" of 1936, and Alan Turing'sTuring machines of 1936–7 and 1939. Giving a formal definition of algorithms, corresponding to the intuitive notion, remains a challenging problem.[11]
Etymology
The word 'algorithm' probably has its roots in latinizing the name of Al-Khwarizmi in a first step to algorismus.[12][13]. There is no prior root for algorism- or algorit-, neither in Latin, nor in Greek. The word seems to have evolved as the name for the "new" mathematics coming to Europe, characterized by the use of the then emerging Arabic numerals, and was probably influenced by the Greek wordarithmos, i.e. αριθμός, meaning "number" (cf.arithmetics), leading to the "t" in algorithm.
Al-Khwārizmī (Persian: خوارزمی, c. 780–850) was a Persian mathematician, astronomer,geographer, and scholar in the House of Wisdom in Baghdad, whose name means 'the native of Khwarezm', a region that was part ofGreater Iran and is now in Uzbekistan.[14][15]About 825, he wrote a treatise in the Arabic language, which was translated into Latin in the 12th century under the title Algoritmi de numero Indorum. This title means "Algoritmi on the numbers of the Indians", where "Algoritmi" was the translator's Latinization of Al-Khwarizmi's name.[16] Al-Khwarizmi was the most widely read mathematician in Europe in the late Middle Ages, primarily through another of his books, the Algebra.[17]In late medieval Latin, algorismus, English 'algorism', the corruption of his name, simply meant the "decimal number system". In the 15th century, under the influence of the Greek word ἀριθμός 'number' (cf. 'arithmetic'), the Latin word was altered to algorithmus, and the corresponding English term 'algorithm' is first attested in the 17th century; the modern sense was introduced in the 19th century.[18]
In English, it was first used in about 1230 and then by Chaucer in 1391. English adopted the French term, but it wasn't until the late 19th century that "algorithm" took on the meaning that it has in modern English.
Another early use of the word is from 1240, in a manual titled Carmen de Algorismocomposed by Alexandre de Villedieu. It begins thus:
which translates as:
The poem is a few hundred lines long and summarizes the art of calculating with the new style of Indian dice, or Talibus Indorum, or Hindu numerals.
Informal definition
An informal definition could be "a set of rules that precisely defines a sequence of operations."[19] which would include all computer programs, including programs that do not perform numeric calculations. Generally, a program is only an algorithm if it stops eventually.[20]
A prototypical example of an algorithm is theEuclidean algorithm to determine the maximum common divisor of two integers; an example (there are others) is described by theflow chart above and as an example in a later section.
Boolos, Jeffrey & 1974, 1999 offer an informal meaning of the word in the following quotation:
An "enumerably infinite set" is one whose elements can be put into one-to-one correspondence with the integers. Thus, Boolos and Jeffrey are saying that an algorithm implies instructions for a process that "creates" output integers from anarbitrary "input" integer or integers that, in theory, can be arbitrarily large. Thus an algorithm can be an algebraic equation such as y = m + n – two arbitrary "input variables" mand n that produce an output y. But various authors' attempts to define the notion indicate that the word implies much more than this, something on the order of (for the addition example):
- Precise instructions (in language understood by "the computer")[22] for a fast, efficient, "good"[23] process that specifies the "moves" of "the computer" (machine or human, equipped with the necessary internally contained information and capabilities)[24] to find, decode, and then process arbitrary input integers/symbols mand n, symbols + and = ... and "effectively"[25] produce, in a "reasonable" time,[26] output-integer y at a specified place and in a specified format.
The concept of algorithm is also used to define the notion of decidability. That notion is central for explaining how formal systemscome into being starting from a small set ofaxioms and rules. In logic, the time that an algorithm requires to complete cannot be measured, as it is not apparently related with our customary physical dimension. From such uncertainties, that characterize ongoing work, stems the unavailability of a definition ofalgorithm that suits both concrete (in some sense) and abstract usage of the term.
Formalization
Algorithms are essential to the way computers process data. Many computer programs contain algorithms that detail the specific instructions a computer should perform (in a specific order) to carry out a specified task, such as calculating employees' paychecks or printing students' report cards. Thus, an algorithm can be considered to be any sequence of operations that can be simulated by a Turing-complete system. Authors who assert this thesis include Minsky (1967), Savage (1987) and Gurevich (2000):
Typically, when an algorithm is associated with processing information, data can be read from an input source, written to an output device and stored for further processing. Stored data are regarded as part of the internal state of the entity performing the algorithm. In practice, the state is stored in one or more data structures.
For some such computational process, the algorithm must be rigorously defined: specified in the way it applies in all possible circumstances that could arise. That is, any conditional steps must be systematically dealt with, case-by-case; the criteria for each case must be clear (and computable).
Because an algorithm is a precise list of precise steps, the order of computation is always crucial to the functioning of the algorithm. Instructions are usually assumed to be listed explicitly, and are described as starting "from the top" and going "down to the bottom", an idea that is described more formally by flow of control.
So far, this discussion of the formalization of an algorithm has assumed the premises ofimperative programming. This is the most common conception, and it attempts to describe a task in discrete, "mechanical" means. Unique to this conception of formalized algorithms is the assignment operation, setting the value of a variable. It derives from the intuition of "memory" as a scratchpad. There is an example below of such an assignment.
For some alternate conceptions of what constitutes an algorithm see functional programming and logic programming.
Expressing algorithms
Algorithms can be expressed in many kinds of notation, including natural languages,pseudocode, flowcharts, drakon-charts,programming languages or control tables(processed by interpreters). Natural language expressions of algorithms tend to be verbose and ambiguous, and are rarely used for complex or technical algorithms. Pseudocode, flowcharts, drakon-charts and control tables are structured ways to express algorithms that avoid many of the ambiguities common in natural language statements. Programming languages are primarily intended for expressing algorithms in a form that can be executed by a computer, but are often used as a way to define or document algorithms.
There is a wide variety of representations possible and one can express a given Turing machine program as a sequence of machine tables (see more at finite-state machine, state transition table and control table), as flowcharts and drakon-charts (see more atstate diagram), or as a form of rudimentarymachine code or assembly code called "sets of quadruples" (see more at Turing machine).
Representations of algorithms can be classed into three accepted levels of Turing machine description:[29]
- 1 High-level description
- "...prose to describe an algorithm, ignoring the implementation details. At this level we do not need to mention how the machine manages its tape or head."
- 2 Implementation description
- "...prose used to define the way the Turing machine uses its head and the way that it stores data on its tape. At this level we do not give details of states or transition function."
- 3 Formal description
- Most detailed, "lowest level", gives the Turing machine's "state table".
For an example of the simple algorithm "Add m+n" described in all three levels, seeAlgorithm#Examples.
Implementation
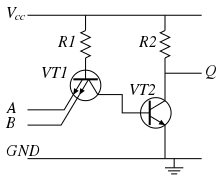
Logical NAND algorithm implemented electronically in 7400 chip
Most algorithms are intended to be implemented as computer programs. However, algorithms are also implemented by other means, such as in a biological neural network (for example, the human brainimplementing arithmetic or an insect looking for food), in an electrical circuit, or in a mechanical device.
Computer algorithms
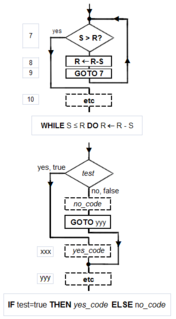
Flowchart examples of the canonical Böhm-Jacopini structures: the SEQUENCE (rectangles descending the page), the WHILE-DO and the IF-THEN-ELSE. The three structures are made of the primitive conditional GOTO (IFtest=true THEN GOTO step xxx) (a diamond), the unconditional GOTO (rectangle), various assignment operators (rectangle), and HALT (rectangle). Nesting of these structures inside assignment-blocks result in complex diagrams (cf Tausworthe 1977:100,114).
In computer systems, an algorithm is basically an instance of logic written in software by software developers to be effective for the intended "target" computer(s) to produce output from given (perhaps null)input. An optimal algorithm, even running in old hardware, would produce faster results than a non-optimal (higher time complexity) algorithm for the same purpose, running in more efficient hardware; that is why algorithms, like computer hardware, are considered technology.
"Elegant" (compact) programs, "good" (fast) programs : The notion of "simplicity and elegance" appears informally in Knuth and precisely in Chaitin:
- Knuth: ". . .we want good algorithms in some loosely defined aesthetic sense. One criterion . . . is the length of time taken to perform the algorithm . . .. Other criteria are adaptability of the algorithm to computers, its simplicity and elegance, etc"[30]
- Chaitin: " . . . a program is 'elegant,' by which I mean that it's the smallest possible program for producing the output that it does"[31]
Chaitin prefaces his definition with: "I'll show you can't prove that a program is 'elegant'"—such a proof would solve the Halting problem(ibid).
Algorithm versus function computable by an algorithm: For a given function multiple algorithms may exist. This is true, even without expanding the available instruction set available to the programmer. Rogers observes that "It is . . . important to distinguish between the notion of algorithm, i.e. procedure and the notion of function computable by algorithm, i.e. mapping yielded by procedure. The same function may have several different algorithms".[32]
Unfortunately there may be a tradeoff between goodness (speed) and elegance (compactness)—an elegant program may take more steps to complete a computation than one less elegant. An example that uses Euclid's algorithm appears below.
Computers (and computors), models of computation: A computer (or human "computor"[33]) is a restricted type of machine, a "discrete deterministic mechanical device"[34] that blindly follows its instructions.[35] Melzak's and Lambek's primitive models[36] reduced this notion to four elements: (i) discrete, distinguishablelocations, (ii) discrete, indistinguishablecounters[37] (iii) an agent, and (iv) a list of instructions that are effective relative to the capability of the agent.[38]
Minsky describes a more congenial variation of Lambek's "abacus" model in his "Very Simple Bases for Computability".[39] Minsky's machine proceeds sequentially through its five (or six, depending on how one counts) instructions, unless either a conditional IF–THEN GOTO or an unconditional GOTO changes program flow out of sequence. Besides HALT, Minsky's machine includes three assignment (replacement, substitution)[40] operations: ZERO (e.g. the contents of location replaced by 0: L ← 0), SUCCESSOR (e.g. L ← L+1), and DECREMENT (e.g. L ← L − 1).[41] Rarely must a programmer write "code" with such a limited instruction set. But Minsky shows (as do Melzak and Lambek) that his machine is Turing completewith only four general types of instructions: conditional GOTO, unconditional GOTO, assignment/replacement/substitution, and HALT.[42]
Simulation of an algorithm: computer (computor) language: Knuth advises the reader that "the best way to learn an algorithm is to try it . . . immediately take pen and paper and work through an example".[43] But what about a simulation or execution of the real thing? The programmer must translate the algorithm into a language that the simulator/computer/computor can effectivelyexecute. Stone gives an example of this: when computing the roots of a quadratic equation the computor must know how to take a square root. If they don't, then the algorithm, to be effective, must provide a set of rules for extracting a square root.[44]
This means that the programmer must know a "language" that is effective relative to the target computing agent (computer/computor).
But what model should be used for the simulation? Van Emde Boas observes "even if we base complexity theory on abstract instead of concrete machines, arbitrariness of the choice of a model remains. It is at this point that the notion of simulation enters".[45]When speed is being measured, the instruction set matters. For example, the subprogram in Euclid's algorithm to compute the remainder would execute much faster if the programmer had a "modulus" instruction available rather than just subtraction (or worse: just Minsky's "decrement").
Structured programming, canonical structures: Per the Church–Turing thesis, any algorithm can be computed by a model known to beTuring complete, and per Minsky's demonstrations, Turing completeness requires only four instruction types—conditional GOTO, unconditional GOTO, assignment, HALT. Kemeny and Kurtz observe that, while "undisciplined" use of unconditional GOTOs and conditional IF-THEN GOTOs can result in "spaghetti code", a programmer can write structured programs using only these instructions; on the other hand "it is also possible, and not too hard, to write badly structured programs in a structured language".[46] Tausworthe augments the three Böhm-Jacopini canonical structures:[47] SEQUENCE, IF-THEN-ELSE, and WHILE-DO, with two more: DO-WHILE and CASE.[48] An additional benefit of a structured program is that it lends itself to proofs of correctness using mathematical induction.[49]
Canonical flowchart symbols[50]: The graphical aide called a flowchart offers a way to describe and document an algorithm (and a computer program of one). Like program flow of a Minsky machine, a flowchart always starts at the top of a page and proceeds down. Its primary symbols are only four: the directed arrow showing program flow, the rectangle (SEQUENCE, GOTO), the diamond (IF-THEN-ELSE), and the dot (OR-tie). The Böhm–Jacopini canonical structures are made of these primitive shapes. Sub-structures can "nest" in rectangles, but only if a single exit occurs from the superstructure. The symbols, and their use to build the canonical structures, are shown in the diagram.
Examples
Algorithm example
An animation of the quicksort algorithm sorting an array of randomized values. The red bars mark the pivot element; at the start of the animation, the element farthest to the right hand side is chosen as the pivot.
One of the simplest algorithms is to find the largest number in a list of numbers of random order. Finding the solution requires looking at every number in the list. From this follows a simple algorithm, which can be stated in a high-level description English prose, as:
High-level description:
- If there are no numbers in the set then there is no highest number.
- Assume the first number in the set is the largest number in the set.
- For each remaining number in the set: if this number is larger than the current largest number, consider this number to be the largest number in the set.
- When there are no numbers left in the set to iterate over, consider the current largest number to be the largest number of the set.
(Quasi-)formal description: Written in prose but much closer to the high-level language of a computer program, the following is the more formal coding of the algorithm inpseudocode or pidgin code:
Algorithm LargestNumber Input: A list of numbers L. Output: The largest number in the list L.
if L.size = 0 return null
largest ← L[0]
for each item in L, do
if item > largest, then
largest ← item
return largest
- "←" denotes assignment. For instance, "largest ← item" means that the value oflargest changes to the value of item.
- "return" terminates the algorithm and outputs the following value.
Euclid's algorithm
The example-diagram of Euclid's algorithm from T.L. Heath (1908), with more detail added. Euclid does not go beyond a third measuring, and gives no numerical examples. Nicomachus gives the example of 49 and 21: "I subtract the less from the greater; 28 is left; then again I subtract from this the same 21 (for this is possible); 7 is left; I subtract this from 21, 14 is left; from which I again subtract 7 (for this is possible); 7 is left, but 7 cannot be subtracted from 7." Heath comments that, "The last phrase is curious, but the meaning of it is obvious enough, as also the meaning of the phrase about ending 'at one and the same number'."(Heath 1908:300).
Euclid's algorithm to compute the greatest common divisor (GCD) to two numbers appears as Proposition II in Book VII ("Elementary Number Theory") of hisElements.[51] Euclid poses the problem thus: "Given two numbers not prime to one another, to find their greatest common measure". He defines "A number [to be] a multitude composed of units": a counting number, a positive integer not including zero. To "measure" is to place a shorter measuring length s successively (q times) along longer length l until the remaining portion r is less than the shorter length s.[52] In modern words, remainder r = l − q×s, q being the quotient, or remainder r is the "modulus", the integer-fractional part left over after the division.[53]
For Euclid's method to succeed, the starting lengths must satisfy two requirements: (i) the lengths must not be zero, AND (ii) the subtraction must be “proper”; i.e., a test must guarantee that the smaller of the two numbers is subtracted from the larger (alternately, the two can be equal so their subtraction yields zero).
Euclid's original proof adds a third requirement: the two lengths must not be prime to one another. Euclid stipulated this so that he could construct a reductio ad absurdum proof that the two numbers' common measure is in fact the greatest.[54]While Nicomachus' algorithm is the same as Euclid's, when the numbers are prime to one another, it yields the number "1" for their common measure. So, to be precise, the following is really Nicomachus' algorithm.
Computer language for Euclid's algorithm
Only a few instruction types are required to execute Euclid's algorithm—some logical tests (conditional GOTO), unconditional GOTO, assignment (replacement), and subtraction.
- A location is symbolized by upper case letter(s), e.g. S, A, etc.
- The varying quantity (number) in a location is written in lower case letter(s) and (usually) associated with the location's name. For example, location L at the start might contain the number l = 3009.
An inelegant program for Euclid's algorithm
The following algorithm is framed as Knuth's four-step version of Euclid's and Nicomachus', but, rather than using division to find the remainder, it uses successive subtractions of the shorter length s from the remaining lengthr until r is less than s. The high-level description, shown in boldface, is adapted from Knuth 1973:2–4:
INPUT:
1 [Into two locations L and S put the numbers l and s that represent the two lengths]: INPUT L, S 2 [Initialize R: make the remaining length r equal to the starting/initial/input length l]: R ← L
E0: [Ensure r ≥ s.]
3 [Ensure the smaller of the two numbers is in S and the larger in R]: IF R > S THEN the contents of L is the larger number so skip over the exchange-steps 4, 5 and 6: GOTO step 6 ELSE swap the contents of R and S. 4 L ← R (this first step is redundant, but is useful for later discussion). 5 R ← S 6 S ← L
E1: [Find remainder]: Until the remaining length r in R is less than the shorter length s in S, repeatedly subtract the measuring numbers in S from the remaining length r in R.
7 IF S > R THEN done measuring so GOTO 10 ELSE measure again, 8 R ← R − S 9 [Remainder-loop]: GOTO 7.
E2: [Is the remainder zero?]: EITHER (i) the last measure was exact, the remainder in R is zero, and the program can halt, OR (ii) the algorithm must continue: the last measure left a remainder in R less than measuring number in S.
10 IF R = 0 THEN done so GOTO step 15 ELSE CONTINUE TO step 11,
E3: [Interchange s and r]: The nut of Euclid's algorithm. Use remainder r to measure what was previously smaller number s; L serves as a temporary location.
11 L ← R 12 R ← S 13 S ← L 14 [Repeat the measuring process]: GOTO 7
OUTPUT:
15 [Done. S contains the greatest common divisor]: PRINT S
DONE:
16 HALT, END, STOP.
An elegant program for Euclid's algorithm
The following version of Euclid's algorithm requires only six core instructions to do what thirteen are required to do by "Inelegant"; worse, "Inelegant" requires more types of instructions. The flowchart of "Elegant" can be found at the top of this article. In the (unstructured) Basic language, the steps are numbered, and the instruction
LET [] = [] is the assignment instruction symbolized by ←. 5 REM Euclid's algorithm for greatest common divisor
6 PRINT "Type two integers greater than 0"
10 INPUT A,B
20 IF B=0 THEN GOTO 80
30 IF A > B THEN GOTO 60
40 LET B=B-A
50 GOTO 20
60 LET A=A-B
70 GOTO 20
80 PRINT A
90 END
The following version can be used with Object Oriented languages:
// Euclid's algorithm for greatest common divisor
integer euclidAlgorithm (int A, int B){
A=Math.abs(A);
B=Math.abs(B);
while (B!=0){
if (A>B) A=A-B;
else B=B-A;
}
return A;
}
How "Elegant" works: In place of an outer "Euclid loop", "Elegant" shifts back and forth between two "co-loops", an A > B loop that computes A ← A − B, and a B ≤ A loop that computes B ← B − A. This works because, when at last the minuend M is less than or equal to the subtrahend S ( Difference = Minuend − Subtrahend), the minuend can become s (the new measuring length) and the subtrahend can become the new r (the length to be measured); in other words the "sense" of the subtraction reverses.
Testing the Euclid algorithms
Does an algorithm do what its author wants it to do? A few test cases usually suffice to confirm core functionality. One source[55]uses 3009 and 884. Knuth suggested 40902, 24140. Another interesting case is the tworelatively prime numbers 14157 and 5950.
But exceptional cases must be identified and tested. Will "Inelegant" perform properly when R > S, S > R, R = S? Ditto for "Elegant": B > A, A > B, A = B? (Yes to all). What happens when one number is zero, both numbers are zero? ("Inelegant" computes forever in all cases; "Elegant" computes forever when A = 0.) What happens if negative numbers are entered? Fractional numbers? If the input numbers, i.e. the domain of the function computed by the algorithm/program, is to include only positive integers including zero, then the failures at zero indicate that the algorithm (and the program that instantiates it) is a partial function rather than a total function. A notable failure due to exceptions is the Ariane 5 Flight 501 rocket failure (June 4, 1996).
Proof of program correctness by use of mathematical induction: Knuth demonstrates the application of mathematical induction to an "extended" version of Euclid's algorithm, and he proposes "a general method applicable to proving the validity of any algorithm".[56] Tausworthe proposes that a measure of the complexity of a program be the length of its correctness proof.[57]
Measuring and improving the Euclid algorithms
Elegance (compactness) versus goodness (speed): With only six core instructions, "Elegant" is the clear winner, compared to "Inelegant" at thirteen instructions. However, "Inelegant" is faster (it arrives at HALT in fewer steps). Algorithm analysis[58] indicates why this is the case: "Elegant" does twoconditional tests in every subtraction loop, whereas "Inelegant" only does one. As the algorithm (usually) requires many loop-throughs, on average much time is wasted doing a "B = 0?" test that is needed only after the remainder is computed.
Can the algorithms be improved?: Once the programmer judges a program "fit" and "effective"—that is, it computes the function intended by its author—then the question becomes, can it be improved?
The compactness of "Inelegant" can be improved by the elimination of five steps. But Chaitin proved that compacting an algorithm cannot be automated by a generalized algorithm;[59] rather, it can only be doneheuristically; i.e., by exhaustive search (examples to be found at Busy beaver), trial and error, cleverness, insight, application ofinductive reasoning, etc. Observe that steps 4, 5 and 6 are repeated in steps 11, 12 and 13. Comparison with "Elegant" provides a hint that these steps, together with steps 2 and 3, can be eliminated. This reduces the number of core instructions from thirteen to eight, which makes it "more elegant" than "Elegant", at nine steps.
The speed of "Elegant" can be improved by moving the "B=0?" test outside of the two subtraction loops. This change calls for the addition of three instructions (B = 0?, A = 0?, GOTO). Now "Elegant" computes the example-numbers faster; whether this is always the case for any given A, B and R, S would require a detailed analysis.
Algorithmic analysis
It is frequently important to know how much of a particular resource (such as time or storage) is theoretically required for a given algorithm. Methods have been developed for the analysis of algorithms to obtain such quantitative answers (estimates); for example, the sorting algorithm above has a time requirement of O(n), using the big O notation with n as the length of the list. At all times the algorithm only needs to remember two values: the largest number found so far, and its current position in the input list. Therefore, it is said to have a space requirement of O(1), if the space required to store the input numbers is not counted, or O(n) if it is counted.
Different algorithms may complete the same task with a different set of instructions in less or more time, space, or 'effort' than others. For example, a binary search algorithm (with cost O(log n) ) outperforms a sequential search (cost O(n) ) when used for table lookups on sorted lists or arrays.
Formal versus empirical
The analysis and study of algorithms is a discipline of computer science, and is often practiced abstractly without the use of a specific programming language or implementation. In this sense, algorithm analysis resembles other mathematical disciplines in that it focuses on the underlying properties of the algorithm and not on the specifics of any particular implementation. Usually pseudocode is used for analysis as it is the simplest and most general representation. However, ultimately, most algorithms are usually implemented on particular hardware / software platforms and their algorithmic efficiency is eventually put to the test using real code. For the solution of a "one off" problem, the efficiency of a particular algorithm may not have significant consequences (unless n is extremely large) but for algorithms designed for fast interactive, commercial or long life scientific usage it may be critical. Scaling from small n to large n frequently exposes inefficient algorithms that are otherwise benign.
Empirical testing is useful because it may uncover unexpected interactions that affect performance. Benchmarks may be used to compare before/after potential improvements to an algorithm after program optimization. Empirical tests cannot replace formal analysis, though, and are not trivial to perform in a fair manner.[60]
Execution efficiency
To illustrate the potential improvements possible even in well established algorithms, a recent significant innovation, relating to FFTalgorithms (used heavily in the field of image processing), can decrease processing time up to 1,000 times for applications like medical imaging.[61] In general, speed improvements depend on special properties of the problem, which are very common in practical applications.[62] Speedups of this magnitude enable computing devices that make extensive use of image processing (like digital cameras and medical equipment) to consume less power.
Comments
Post a Comment